30 Design Strategies and Tactics from 40 Years of Investigation
Appendix: Further information and examples
Design for ‘role-shifting’
Every classroom has a ‘contract’, usually implicit, between the teacher and the students as to what each will do, what roles they will fulfill. In most mathematics classrooms, the teacher plays directive roles (manager, explainer, task setter, answer provider) while the students play passive imitative roles, listening to the teacher's explanations (not always attentively!) and imitating in a series of repetitive exercises the procedures that the teacher has just demonstrated in working through an example. Students soon learn that the worked example is the key for what they have to do. (Indeed there is much to be said for delaying the explanation until after the examples.) Teaching and learning mathematics this way does not develop students' ability to ‘do mathematics’ themselves.
For that they need to develop autonomy in developing chains of reasoning and solving problems. The teacher needs to ‘get out of the way’ to make room for the students to make the mathematics they do their own – and to and encourage and support this ‘from the side’. This implies a shift of roles with teachers shifting from the directive roles to more facilitative ones, sometimes described (Phillips 1988) as counsellor, fellow student, and resource – providing information only on demand. Students in turn become explainers and play a role in task-setting – an important part of an inquiry-based approach. Teacher interventions are mainly in the form of non-directive questions. (See Common issues tables)
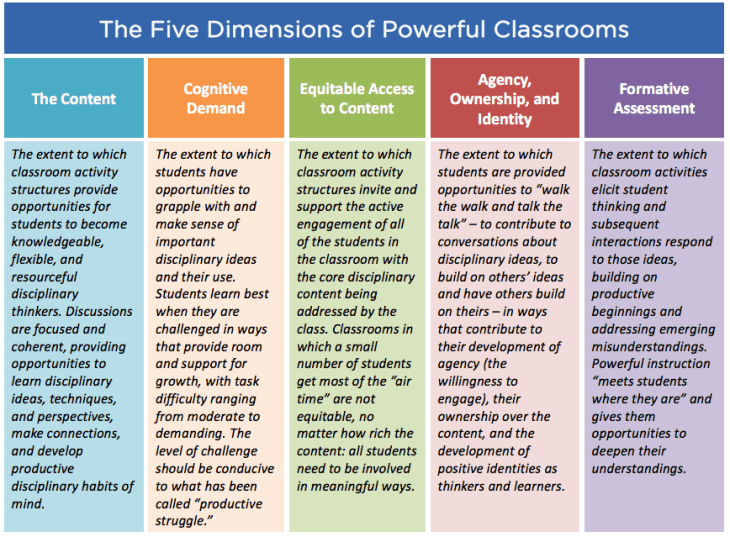
Teaching for Robust Understanding (TRU)
TRU provides a broader framework on this issue. It identifies five dimensions that characterise classrooms that develop mathematically powerful students. Such classrooms provide positive answers to these questions:
Link to TRU website
- The discipline: Are students engaged with and in important content and practices?
- Cognitive demand: Do activities involve students in productive struggle?
- Access: Are all the students actively involved in each phase of learning activities?
- Agency, ownership and identity: Does each student feel that they can contribute and that their mathematical reasoning is recognized as “belonging to them” and their fellow students?
- Formative assessment: Is instruction structured to consistently reveal student thinking and provide formative feedback?
Dimensions 2, 3,4 and 5 all require a shift in roles from traditional mathematics classrooms, with students taking more responsibility – and doing much of the explaining of the mathematics. Each of the dimensions is “actionable” by designers.
The design of most of the examples used in the strategies and tactics described in this article represent role shifting in one way or another.
Links to materials:
- Teaching for Robust Understanding
- https://truframework.org/