30 Design Strategies and Tactics from 40 Years of Investigation
Appendix: Further information and examples
Exemplars communicate vividly
The following examples allow the reader to explore the way specific tasks reduce ambiguity inherent in (fairly standard) descriptions of:
- Student understanding
- Problem solving performance
The same principle is generally true, e.g. for explanations, but the examples would be longer.
Student understanding
"We teach our students to understand the arithmetic of odd and even numbers"
The following examples are teacher questions/instructions that address this issue at different levels.
Example 1
If you add an odd number and an even number, is the answer odd or even?
Example 2
Why is the sum of two odd numbers an even number?
Example 3
Find patterns in the addition of odd and even numbers. Explain why they are always true.
Now find and justify the patterns for multiplication of odds and evens.
Problem solving
“Problem solving is an important part of our mathematics curriculum.”
Example 1a – from anywhere!
If it takes 3 men 5 hours to dig a ditch 80 metres long, how long will it take 4 men to dig a ditch 300 metres long?
Example 1b – from “Nine Chapters on the Mathematical Art” - China, approx. 200BC
A cistern is filled through five canals. Open the first canal and the cistern fills in ⅓ day; with the second, it fills in 1 day; with the third, in 2½ days; with the fourth, in 3 days, and with the fifth in 5 days. If all the canals are opened, how long will it take to fill the cistern?
Example 2 – from Balanced Assessment in Mathematics test for Grade 3 2009
Enlarge…
Link to full PDF
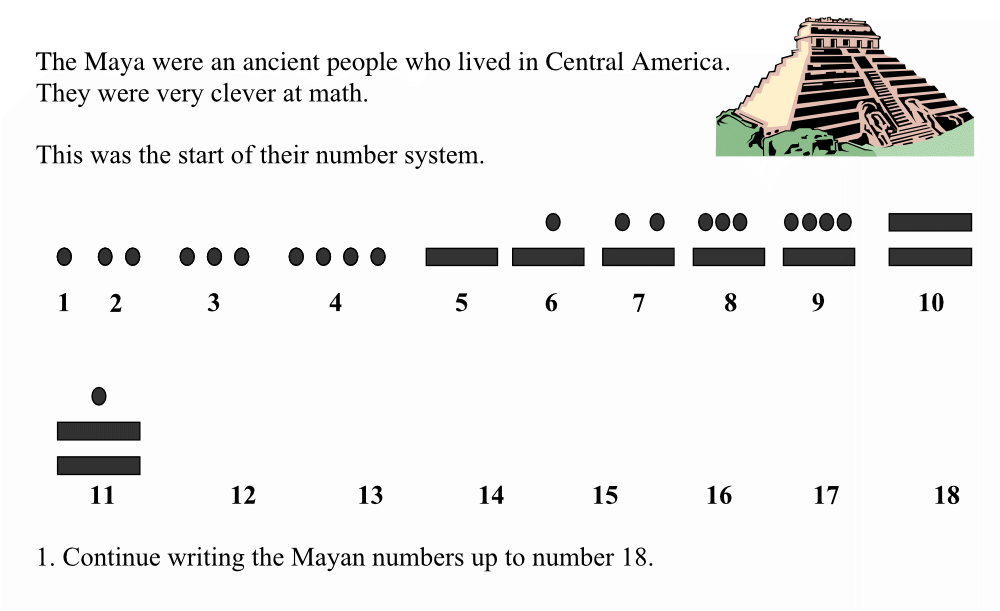
Mayan numbers


Example 4 from Problems with Patterns and Numbers

Link to the PPN materials
This module included a much fuller description of what was meant by problem solving:
This Module introduces a somewhat new type of examination question in which the mathematical processes involved, especially the choice and explanation of strategies and discussion of results, are as important as the answers obtained. This is reflected in the marking schemes.
The questions set will be drawn from a wide variety of problems which are loosely linked under the heading "Patterns and Numbers". The range of problems is not defined in the conventional way by specifying a topic area or listing the mathematical techniques involved. Instead, the problems will involve situations in which, starting from the consideration of some particular cases, a pattern has to be found and then formulated into a general rule. These processes are important throughout mathematics and number properties and patterns provide a suitable field in which they can be developed. The questions in this sample would take up about 20 minutes of examination time.
We invite the reader to think of tasks that they think fit this description before looking at the examples in the module at pages 10-37 of https://www.mathshell.com/publications/tss/ppn/ppn_teacher.pdf
How far do the examples of student work, unscored and scored, further narrow the ambiguity?
Links to materials:
- Mayan Numbers
- http://educationaldesigner.org/ed/volume4/issue13/article53/links/materials/mayan_numbers.pdf
- Making Matchsticks
- https://www.map.mathshell.org/lessons.php?unit=8300&collection=8
- Problems with Patterns and Numbers
- https://www.mathshell.com/materials.php?item=ppn&series=tss






