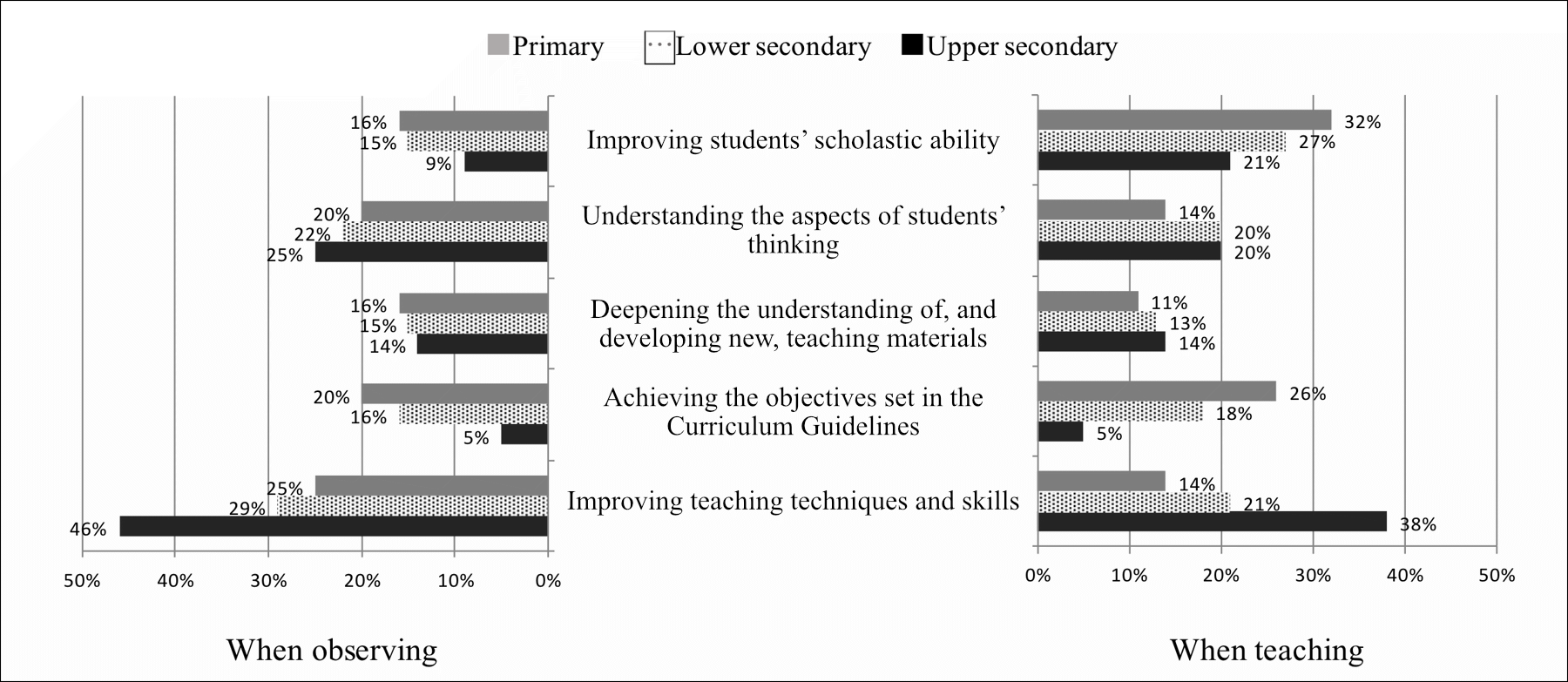
Third, upper secondary teachers have different purposes for research lessons. Figure 1 shows the five “primary purposes” for observing or teaching a research lesson, that were most frequently selected from the following options: achieving the objectives set in the Curriculum Guidelines; improving the textbook and curriculum; deepening the understanding of, and developing new, teaching materials; improving the teaching techniques and skills of teachers; understanding the aspects of students’ thinking; evaluating students; improving students’ scholastic ability; better preparing for entrance exams; accountability to parents and the local community.

Lesson Study at Upper Secondary Level in Japan
Potential and Issues
Keiichi Nishimura*, Ren Kobayashi**, Shinya Ohta*
* Tokyo Gakugei University
**Tokyo Gakugei University International Secondary School
Abstract
iIt is well known that Lesson Study is deeply rooted in school education in Japan. Though Lesson Study is seen at upper secondary level in Japan, it is different from that at primary and lower secondary levels. In many case at upper secondary level, Lesson Study focuses on the “mathematical content” of the lesson or “teaching skill” for explaining the solutions. This paper examines in detail Lesson Study at year 12 of the Project IMPULS (International Math-teacher Professionalization Using Lesson Study) Lesson Study Immersion Program in 2014. The teacher focused on the process of problem-solving for measures against an infectious disease. Based on the lesson plan and teacher practice, especially student activities, we identify the possibilities of and issues concerning Lesson Study at upper secondary level.
Introduction
iiIt is well known that Lesson Study is deeply rooted in school education in Japan. Its use around the world grew following the publication of “The Teaching Gap” by Stigler and Hiebert in 1999. However, Lesson Study at upper secondary level has not yet developed to the same extent as at primary and lower secondary levels in Japan. In this paper, first we show the results of our survey on Lesson Study for Japanese teachers and consider the differences of Lesson Study at primary, lower and upper secondary levels. Next, we examine Lesson Study at a high school as a case study, and discuss the possibility of high-quality Lesson Study at upper secondary level.
Lesson Study at Senior High School in Japan
1Fujii (2016) defines the process of Lesson Study as follows:
- Goal setting. Consider long-term goals for student learning and development. Identify gaps between these long-term goals and current reality. Formulate the research theme.
- Lesson planning. Collaboratively plan a “research lesson” designed to address the goals. Prepare a “lesson proposal”—a document that describes the research theme, content goals, connections between the current content and related content from former and later grades, rationale for the chosen approach, a detailed plan for the research lesson, anticipated student thinking, data collection, and more.
- Research lesson. One team member teaches the research lesson while the other members of the planning team, staff members from across the school, and, usually, an outside knowledgeable other, observe and collect data.
- Post-lesson discussion. In a formal lesson colloquium, observers share data from the lesson to illuminate student learning, disciplinary content, lesson and unit design, and broader issues in teaching and learning.
- Reflection. Document the cycle to consolidate and carry forward learnings, as well as new questions for the next cycle of Lesson Study. Write a report or bulletin that includes the original research lesson proposal, student data from the research lesson, and reflections on what was learned.
The “research lesson” is the core of the system. The research theme, lesson plan, detailed observation, post-lesson discussion and reflection are also considered to be essential elements of Lesson Study.
IMPULS (International Math-teacher Professionalization through Lesson Study) conducted the “Research Study on the Implementation of Research Lessons in Mathematics” in order to shed light on Lesson Study in mathematics at primary and secondary schools in Japan (Nishimura, Matsuda, Ohta, Takahashi, Nakamura, Fujii, 2013). The survey was conducted in 2012 with a stratified two-step extraction method to select a total of 2,680 schools. We requested responses from primary school teachers belonging to the mathematics department for school duty purposes, and from secondary school mathematics teachers. The response rate was 40.8% (408) for primary schools, 40.5% (405) for lower secondary schools and 46.5% (316) for upper secondary schools.
The findings point to the following situation of research lessons in mathematics at upper secondary school. First, 55% of the research lessons had no research theme, while 22% lacked post-lesson discussion. Second, among the items to be included in the lesson plan, the widest gaps between the primary and lower secondary schools on the one hand and the upper secondary schools on the other were found in “anticipated students’ response,” “problem for the lesson” and “blackboard writing plan.” In particular, 90% of the primary school teachers and 81% of the lower secondary school teachers included “anticipated students’ response” in the lesson plan, whereas only 38% of the upper secondary school teachers did so. The lack of “problem for the lesson” at the upper secondary school level might be explained by the fact that teachers did not feel compelled to include it in the plan as their lesson closely followed the problems presented in the textbook or other teaching materials.
In observing a research lesson, most teachers cited “improving the teaching techniques and skills of teachers” as the primary objective at every educational level, with almost half of the upper secondary school teachers (46%) choosing this answer. The percentage of teachers selecting this option when actually teaching the lesson differed substantially among the educational levels, ranging from 14% at primary school, 21% at lower secondary school to 38% at upper secondary school.
An analysis of the constructed response answers to the question “What are the most important things you have learned through the research lesson in mathematics?” indicates that over 30% of upper secondary school teachers referred to the “significance of research lessons” or “self-awareness”.
The above findings indicate that many cases of Lesson Study at upper secondary school in Japan do not meet Fujii’s definition of (1)~(5) mentioned above.
Does this mean that they are trying, but failing, to replicate the type of Lesson Study conducted at primary and lower secondary levels? If so, what are the obstacles they face? Is it even possible to replicate at upper secondary school the type of Lesson Study conducted at primary and lower secondary levels? The following section examines a case of Lesson Study at an upper secondary school intended to apply and re-create mathematics, and considers the possibilities and challenges for conducting such “mathematical activities.”
Planning activities to apply and re-create mathematics
iiiThe Lesson Study presented below was led by the mathematics department of Tokyo Gakugei University International Secondary School (TGUISS). We focus on the realization of “mathematical activities,” i.e. applying and re-creating mathematics. (See, for example, Becker and Shimada, 1997; Freudenthal, 1968; Shimada, 1977). Shimada (1977) defines “mathematical activities” as the “totality of math-related thinking activities such as thinking to understand the existing mathematical theories, thinking to develop a new theory, and trying to apply mathematics to something in order to solve a non-mathematical problem (p. 14), and demonstrates the concept in a pattern diagram. The purpose of mathematical activities is now gaining further attention in the Japanese mathematics education community.
Our previous lesson studies found that the importance of mathematical activities lay not only in how to realize them, but also in how to ensure their quality. Thus, we defined our research theme as “developing the means of improving the activities to apply and re-create mathematics.” Under this research theme, we decided to conduct Lesson Study on the learning of differential equations, an optional topic for 12th graders. We set the teaching objective of developing the ability of mathematical modelling with differential equations. In particular, we focused on having the students “re-create” the idea of expressing a change in a differential equation in the context of a real-world problem.
Our target was 12th graders (Year 3 in upper secondary school) who have already learned about sequence and recursive formulae, exponential functions, differential coefficients, and derivatives. They also have frequently experienced mathematical modeling activities, since the mathematics department of TGUISS has compiled a textbook focusing on mathematical modelling.
Developing the problem
1We held six sessions for problem setting and lesson proposal drafting, with the participation of mathematics teachers from TGUISS (eight) and other schools affiliated to Tokyo Gakugei University (10 on average).
The class teacher first proposed as a problem the change in water level after piercing a hole in the bottom of a plastic bottle. After discussion, however, we decided not to use this because it was not fit for a lesson oriented towards re-creating mathematics as the teacher would have to explain to the students Torricelli’s law as the key to solving this problem.
Instead, we proposed the SIR Model, which is a classical mathematical model for infectious diseases (Kermack & McKendrick, 1927). Building teaching materials on the SIR Model was considered appropriate for the following reasons. Firstly, differential equations can function efficiently in this example. Secondly, the problem focuses attention on the very change from the susceptible population into the infected/infectious population. Finally, the infected/infectious population at the outset of the epidemic may be described by the linear first-order differential equation, which is also effective for describing other phenomena.
Next, we discussed what kind of ingenuity would be necessary in the problem to allow students who have not learned about differential equations to create a model that may be expressed by the differential equation (where indicates the number of the infected/infectious at time t, and k is a constant).
The discussion led us to make two adjustments to enable students to simulate the change in the number of infected/infectious people and realize the necessity of creating a differential equation for this purpose. The first adjustment was to put the students in the position of the person responsible for public health, to make them feel compelled to simulate the number of infected/infectious people and take action. The second adjustment was to set conditions for simulating the weekly change; it was expected that after simulating the weekly change, the students would feel compelled to look into changes at shorter intervals as the person responsible for public health. We posed the problem shown in Figure 2 in the first of a series of lessons. We allocated a total of five lessons (50 minutes × 5) for solving this problem. The fourth of the five lessons was designated as a research lesson as it addressed the core of the research theme.
Preventing the epidemic of an infectious disease
A person infected by an infectious disease joins a population of 100,000. This disease can transmit the infection to 1.8% of the susceptible population following contact with infected/infectious people, who retain the infectious capacity for one week. Those who have lost the infectious capacity (recovered) acquire immunity to this infectious disease.
You are responsible for the public health of this population, and thus wish to encourage vaccination in anticipation of the epidemic. A survey result indicates that an average person in this population makes contact with 70 people per week.
- Simulate weekly changes in the number of infected people if no action is taken.
- Due to the risk of side effects, it is not practical to vaccinate the whole population. Determine what percentage of the 100,000 population should be vaccinated to prevent the epidemic.
Helping students create a model
2We considered the means of making the students create a model to be expressed by the differential equation dI(t)/dt = kI. Our discussion focused on the following two means. The first means is to “have a recursive formula reconsidered as a difference equation” (hereafter “Means I”). We thought that the students would be inspired to express the change itself as a mathematical formula by regarding an+1 – an = f(n) as a difference equation with respect to the sequence {an}. Hereafter, the sequence {an} refers to the number of infected/infectious people in week n. The second means is to “provide experience in reducing the time interval of the change” (hereafter “Means II”). This is intended to get the students to transform a difference equation into a differential equation. Our idea was that any need to reduce the time interval for a difference equation would ultimately lead the students to create a differential equation.
In class, we decided to actualize the above two means into the following two hatsumon (the thought-provoking question). Hatsumon 1 corresponds to Means I, and Hatsumon 2 to Means II. We also anticipated students’ response to the hatsumon and shaped neriage (whole class discussion phase of structured problem-solving) in its light.
- Hatsumon 1:
- “We must minimize the weekly increment in the infected/infectious if we are to prevent the epidemic. What information can we obtain on the weekly increment in the infected/infectious from the initial epidemic stage of the simulation?”
Anticipated students’ responses:
- S1-1: Calculate the actual weekly increment in the infected/infectious and examine the differences and ratios (analysis of values).
- S1-2: Make a judgment from the shape of a chart plotting the values of the weekly increment in the infected/infectious (analysis of a chart).
- S1-3: Use the general term an = 1.26n to create an+1 – an (analysis of a general term).
- S1-4: Use an+1 = 1.26an to create an+1 – an (analysis of a recursive formula).
Teachers expect that S1-3 and S1-4 may not come spontaneously. In that case, building on S1-2, we will seek to induce a response such that the weekly increment in the infected/infectious resembles the change in the number of the infected/infectious, for example, in discussing the weekly increment in the infected/infectious with the whole class. Even if we manage to create the formula In+1 – In = 0.26In it would be difficult for students to interpret the formula as indicating “the weekly increment in the infected/infectious in proportion to the number of the infected/infectious in the given week.” Thus, the teacher will ask the students about the functional relationship between the weekly increment in the infected/infectious (In+1 – In) and the number of the infected/infectious (In) whilst interacting with the whole class.
- Hatsumon 2:
- “How might we obtain deeper insight into the ever-changing number of the infected/infectious to maximize the accuracy of the preventive measure?”
Anticipated students’ response:
- S2-1: We can make a continuous chart if we can obtain real-time data on the number of the infected/infectious.
- S2-2: We do not need to consider the instantaneous change as we are counting the number of people.
- S2-3: It would be only practical to measure the number of the infected/infectious on a daily basis.
For this neriage, we expected a sublation of two ideas. The first idea, as with S2-1, would ideally call for obtaining a continuous change, while the second idea would reject the need (or possibility) of obtaining any continuous change, as in the case of S2-2. We expected that this sublation would result in the conclusion that it is possible to identify the daily, if not instantaneous change. If we succeed through this discussion in inspiring the students to reduce the time interval from one week to one day, then we will be able to reduce it to an extreme with idealization and simplification.
Report on Lessons 1 through 3
ivHere, the events during the teaching of the first three lessons are briefly summarized. In Lesson 1, students asked some questions about the problem posed by the teacher, which was an essential assumption of the SIR Model. The questions included asking whether they could assume that the population will not change in size or composition. Decisions on such assumptions were made by the whole class to ensure uniformity. The students then moved to discussion in small groups. “Looks like a sequence” and “…the recurrence formula…” were some of the remarks heard towards the end of the lesson.
In Lesson 2, the students continued with problem-solving for the first 20 minutes, followed by a presentation by each group. These are summarized in Table 1. After the group presentations, the two groups that had not expressed their ideas in a recursive formula (Groups 4 and 5) tried to interpret the recursive formulae expressed by Groups 2 and 3. Meanwhile, Groups 2 and 3 proceeded with simulation using their own recursive formula on the spreadsheet. Group 2 identified the cumulative number of infected/infectious people and the week with the largest number of the infected/infectious.
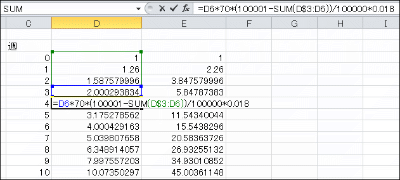
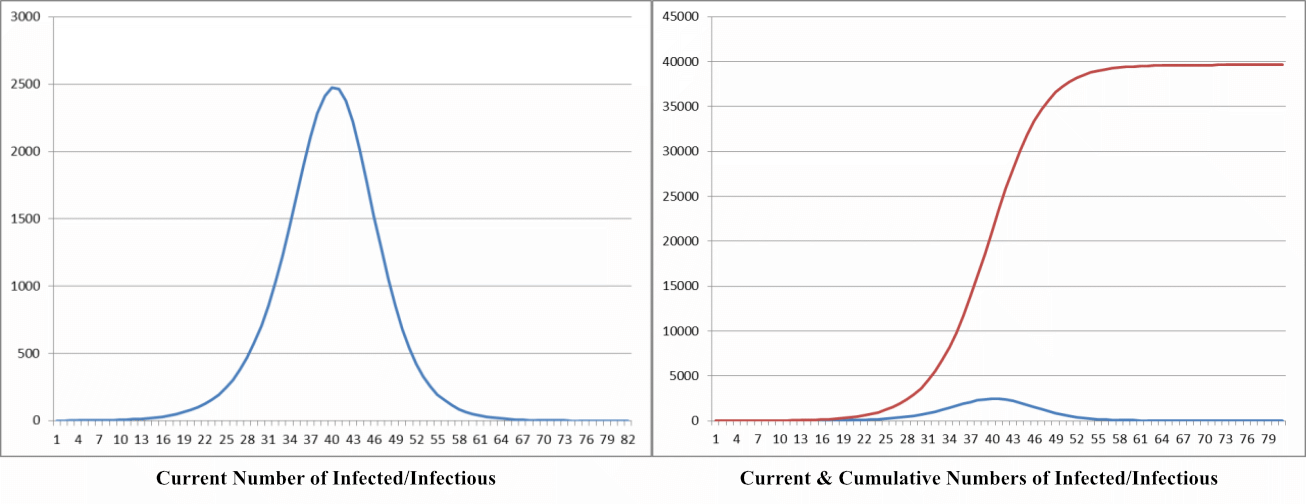
At the beginning of Lesson 3, each group was asked how it intended to solve the problem. As it turned out, all groups were going to adopt the recursive formulae presented by Groups 2 and 3 (the difference being whether the initial week is counted as Week 0 or Week 1). Then, Group 2 was asked to present the method and result of the simulation in the form of a spreadsheet. This is shown in Figure 3. The other groups were also instructed to perform the same operation.
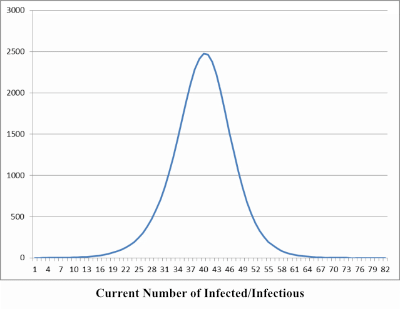
The teacher asked students whether they had drawn a chart similar to those shown in Figure 4: “What kind of chart did you draw?” “A line chart” was the answer. This confirmed that their calculations were on a weekly basis. The teacher then asked: “Is it possible to characterize mathematically the change at the initial stage of the epidemic when the infected/infectious increase in number?” This question was intended to induce the idea that the change in the number of the infected/infectious at the initial stage of the epidemic may be considered as an exponential function. Indeed, students immediately referred to “exponential function.” They made a scatter diagram of the initial increase stage and approximated it with an exponential function.
Next, the teacher asked what kind of change it was in terms of sequence. “Geometric sequence” was the answer. The teacher asked a further question: “How do you know that a geometric sequence is relevant in this case?” The student who had presented the recursive formula for Group 3 in Lesson 2 answered: “No, the common ratio is going to change”. On hearing this, a student in Group 5 remarked: “Since the number of the infected at the initial stage is so small in comparison with the total population of 100,000, (provided
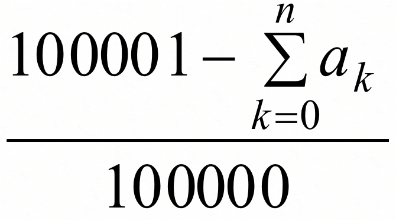 in the recursive formula approximates 1), it may be regarded as a geometric sequence where an+1 equals an multiplied by a constant factor. Based on this remark, we concluded that it was relevant to regard the change in the number of infected/infectious people as a geometric sequence.
in the recursive formula approximates 1), it may be regarded as a geometric sequence where an+1 equals an multiplied by a constant factor. Based on this remark, we concluded that it was relevant to regard the change in the number of infected/infectious people as a geometric sequence.
Report of the Research Lesson 4
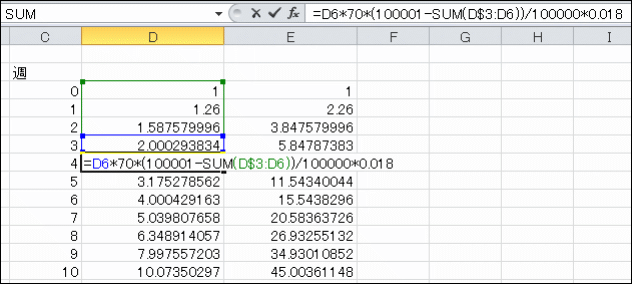
vSome 40 external participants attended the open research lesson, following lessons 1 to 3 above. The teacher started with Hatsumon 1 (see above). In the group solution activity, actual students’ responses included S1-1, S1-2 and S1-3 mentioned above. Then Group 5 presented their idea, as shown in Figure 5.
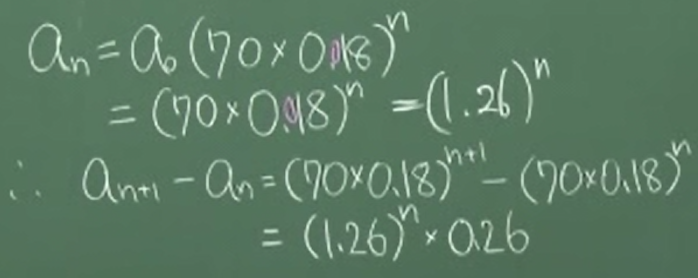
Based on the number of the infected/infectious calculated on a spreadsheet in the previous lesson, we calculated the weekly change in the number of the infected/infectious (weekly increment) and presented it on a chart. The chart helped us realize that the trajectory of the weekly increment resembled that of the number of the infected/infectious. Further investigation using general terms found that the same general term appeared in the sequence for the number of the infected/infectious and that for the weekly increment.
Following this presentation, the teacher started to discuss the meaning of the formula an+1 – an = 0.26an. First, the teacher confirmed that the formula an+1 – an = (1.26)n × 0.26 written on the blackboard should be read as meaning an+1 – an = 0.26an. Then the teacher asked: “What does this formula mean in the context of the present problem?” The students answered: “The weekly increment in the infected/infectious may be expressed as a geometric sequence,” and also “The weekly increment amounts to the number of the infected/infectious multiplied by 0.26.” However, no one observed that the weekly increment in the infected/infectious is proportional to the number of the infected/infectious in the given week. That interpretation came only after the teacher expressed the relationship as y = 0.26x, where y represents the weekly increment in the infected/infectious, and x the number of the infected/infectious in the given week.
Then, the teacher went on to Hatsumon 2. “Do you see any problem in continuing to think only of the weekly change?,” asked the teacher, but the question failed to elicit any response from the students. The teacher then asked a question of a student in Group 4, who sought to consider the daily change from the outset: “Don’t you need to look any more into the daily change in the number of the infected/infectious, which is something you were trying to do in the previous lesson?” The student replied “It’s better to think in daily terms if you want to find out about the change in the number of infectious people, but it’s easier to think in weekly terms because now we are looking at the total of the infected/infectious”. Asked about the reason for the initial attempt to look into the daily change, the student said: “The persons infected on Monday will be recovered by the following Monday. Although more persons will be infected on Tuesday, they will also be recovered by the following Tuesday. I thought the daily change would better capture this course of events.” The teacher then asked the whole class: “How about this idea? With weekly data, you will never know on which day of the week the infection occurred, will you?” Other students joined in: “If that’s the case, it is also true that you will never know when the infection occurred on a given day. You will have to go that far to be exact.” Another student commented: “Even if we consider the daily change, the timing of recovery will depend on whether the person was infected in the morning or in the evening. Thinking in daily terms would be irrelevant.” The teacher concluded the lesson by asking the whole class once again to consider these views.
Post-lesson discussion
1The class teacher self-assessed the lesson at the start of the post-lesson discussion. The assessment focused on the failure to reconsider the recursive formula in Means I as a difference equation. The lesson only managed to use the general term of an = 1.26n to establish the relationship of an+1 – an = 0.26an. The means proved insufficient for inducing the reaction of S1-4 above, or the creation of the recursive formula an+1 = 1.26an as an+1 – an = 0.26an.
The five observers followed with their comments, two of which were particularly noteworthy. One of them concerned Means I. This observer suggested that the students struggled to interpret the formula an+1 – an = 0.26an as meaning that “the weekly increment in the infected/infectious is proportional to the number of the infected/infectious in the given week” because they took the question too seriously. However, nobody could present evidence to that effect. (We subsequently checked with the students on this point, and found that when the teacher asked them about the meaning of the equation, no one was aware that the weekly increment in the infected/infectious is proportional to the number of the infected/infectious in the given week. As it turned out, it was difficult for the students to recognize this.)
Another comment concerned Means II, which questioned whether there was any benefit or necessity in expressing this problem as a differential equation, for a differential equation and a difference equation would lead to the same conclusion on the vaccination rate in Question (2). Thus, this observer argued that it might not be necessary to use a differential equation in this case.
Comments and advice from the koshi
2The koshi (knowledgeable other) noted a couple of issues on aspects of students’ thinking during the lesson. The first issue was: Why is it necessary to interpret an+1 – an = 0.26an as meaning that “the weekly increment in the infected/infectious is proportional to the number of the infected/infectious in the given week?” The students did not recognize what the number of the infected/infectious depends on. The koshi noted that the worksheets and feedback of students indicated that they were thinking in terms of the range of n that allows us to consider the fractional term in the recursive formula
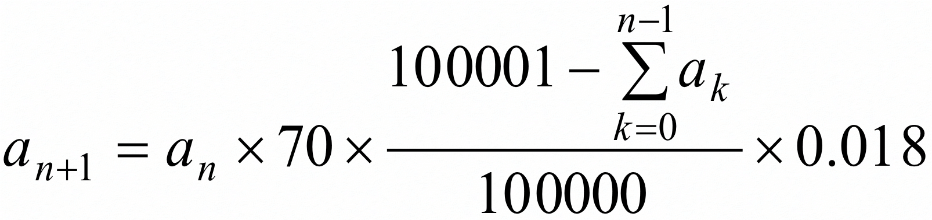 as very close to 1, or in other words “how to reduce the value of p in an+1 = pan to less than 1 because that would prevent {an} from increasing.” Even so, it might have been possible to leverage that awareness for making the students recognize “what the weekly increment in the infected/infectious depends on.” It should also be noted that when the students were encouraged to examine the weekly increment in the infected/infectious, they were not only looking at the recursive formula or general term but were also reverting to the events, tables and charts. Although such reaction had been anticipated to some extent (S1-1 to S1-3), not enough consideration had been given to the means of making the students think in terms of “what the weekly increment in the infected/infectious depends on.” Further consideration of such means may help bring that awareness to the students.
as very close to 1, or in other words “how to reduce the value of p in an+1 = pan to less than 1 because that would prevent {an} from increasing.” Even so, it might have been possible to leverage that awareness for making the students recognize “what the weekly increment in the infected/infectious depends on.” It should also be noted that when the students were encouraged to examine the weekly increment in the infected/infectious, they were not only looking at the recursive formula or general term but were also reverting to the events, tables and charts. Although such reaction had been anticipated to some extent (S1-1 to S1-3), not enough consideration had been given to the means of making the students think in terms of “what the weekly increment in the infected/infectious depends on.” Further consideration of such means may help bring that awareness to the students.
The second issue raised by the koshi was why is it necessary to regard the change in the number of the infected/infectious people as a continuous function. This case tried to reduce the time interval starting from the discrete transition identified by using a sequence, but the change itself remains the same even if it becomes continuous. The students had already observed how the number of the infected/infectious changed on a weekly basis by plotting it on a chart. Although the students prepared line charts, they might have detected a continuous change on those charts. If so, any attempt to reduce the time interval would be irrelevant to them. In any case, it was not necessary for the students to think of the change in the number of the infected/infectious in terms of a continuous function. One observer made a remark on the comment and advice described above: “As it is, the formula an+1 – an = (1.26)n × 0.26 would hardly imply a derivative; to see a derivative it would therefore be necessary to show that the left-hand side actually has (n + 1) – n as a denominator in a tangible manner” 
Reflections and recommendations
viThis section considers the feasibility of, and challenges for Lesson Study at upper secondary school. Lesson Study in Japan is characterized by its integration into the traditional vision of teaching focusing on constructive learning through interaction in class. However, the anticipated response of students is not described in many lesson plans at upper secondary school, as indicated in Section 2. This is partly because schools are not aiming to give lessons that would require such anticipation.
Thus, we review the case to see if it has achieved its stated objective: “lessons that raise the quality of activities to apply and re-create mathematics, building on the activities that the students are supposed to be already capable of.”
In the present case, the students were able to conduct a simulation by developing relevant recursive formulae. In the following lesson, we explained why they were asked if the time interval should be shortened, and showed the formula 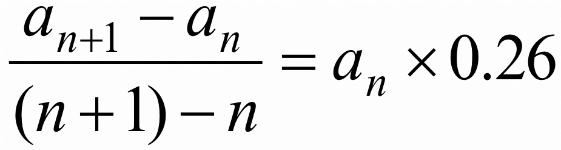 Indeed, they recognized a derivative and managed to rewrite it as a differential equation. These observations indicate that lessons to apply and re-create mathematics with minutely planned problems and means are feasible at upper secondary school.
Indeed, they recognized a derivative and managed to rewrite it as a differential equation. These observations indicate that lessons to apply and re-create mathematics with minutely planned problems and means are feasible at upper secondary school.
To assess the effectiveness of means, it is also imperative to review the post-lesson discussion and the comments and advice by the koshi. After all, the purpose of this Lesson Study was to assess the effectiveness of the means of raising the quality of activities to apply and re-create mathematics. Some views on the means were expressed in the post-lesson discussion. They imply that the type of discussion made at primary and lower secondary levels is also feasible at upper secondary school, provided that the research theme is clear enough. At the same time, however, those views were evidenced in the flow of the lesson, whereas any judgment on the effectiveness of means should be made based on evidence of students’ thinking process in class. The lack of evidence regarding students’ thinking process may be partly because mathematics teachers at upper secondary school do not realize the necessity of such evidence, but some other factors may also be relevant. Problems at upper secondary level are far more complex than those at primary or lower secondary school, reflecting the higher level of mathematics taught. In addition, students think faster and give much longer descriptions and remarks in discussions. Those factors might be addressed to some extent by disclosing the lesson plan in advance to participants so that they can fully understand the anticipated responses of students, or by leveraging digital equipment. Such measures may also help improve the present condition, as indicated in Section 2, where attention is specifically focused on the teacher’s teaching techniques and skills.
In contrast, the koshi pointed out some issues found in the lesson, citing students’ thinking process as evidence. In this respect, the koshi served as a “role model” for the observers of Lesson Study. It is doubtful, however, if the actual participants recognized this. A koshi should also be required to comment on the importance of using students’ thinking process as evidence.
Thus, Lesson Study at upper secondary school may be expected to transform the vision of teaching among teachers by enabling them to focus on the students’ thinking process. Indeed, the vision of problem-solving-oriented teaching among primary school teachers in Japan has been enhanced by the focus that Lesson Study puts on various aspects of children’s thinking.
Conclusion
viiThe case study revealed that upper secondary school lessons aimed at constructive learning through interaction in class are feasible with minutely planned problems and means, and that the kind of Lesson Study conducted at primary and lower secondary schools in Japan can also work at this level. It also noted the following requirements for Lesson Study at upper secondary level: to ensure that the participants in the research lesson fully understand the lesson plan in advance; to leverage digital technology for recording the thinking process of students; and to ensure that the koshi makes comments to the participants on the significance of using students’ thinking process as evidence.
Describing and reviewing the process of Lesson Study, as explained above, can help recognize the takeaways from Lesson Study. Disclosing those takeaways will be the key to the continuation of Lesson Study because it leads to shared understanding of the mechanism by which Lesson Study works.
References
viiiNishimura K., Matsuda N., Ohta S., Takahashi A., Nakamura K., & Fujii T. (2013). Study of Mathematics Research Lesson in Japanese Schools: How Japanese schools use mathematics research lessons for their professional development. Journal of Japan Society of Mathematical Education, 95(6), 2 - 11. (in Japanese)
About the Authors
ix
Keiichi Nishimura is Professor of mathematics education at Tokyo Gakugei university. In his previous capacity as a maths curriculum lead in the National Institute for Educational Policy Research of the Japanese Ministry of Education, Culture, Science and Technology, he became involved in national policy related research and implementation. Today, he continues to work on a wide range of national projects from curriculum revision, assessment, international comparative studies, to work on a leading secondary maths textbook series. As a secondary teacher, he had a track record of research through lesson study on modeling and context rich problems. Today, he guides a number of schools and districts in lesson study to improve their teaching and learning.

Ren Kobayashi is a math teacher at Tokyo Gakugei University International Secondary School. He holds a Ph.D in math education from Tokyo Gakugei University. He is active in lesson study, particularly in realizing "Mathematization". And he is one of the authors of Japanese mathematics textbook series lower secondary level, which will be authorized by the Ministry of Education Japan.

Shinya Ohta is Professor of mathematics education at Tokyo Gakugei University. He is active in lesson study and "kyozai-kenkyu", particularly in realizing Space and Shape. And he is one of the authors of Japanese mathematics textbook series lower secondary level, which will be authorized by the Ministry of Education Japan.